La resolución de problemas plantea una conexión directa con la creatividad al despertar la curiosidad que motiva el aprendizaje y al abrir espacios para la búsqueda de ideas que aporten a la solución de los problemas. Mientras antes entrenemos la creatividad en nuestros estudiantes, antes desarrollaremos su flexibilidad; cuanto antes el aula se transforme en un lugar que acepta y promueve el error como parte del aprendizaje, más se estimula la exploración y se desarrolla del pensamiento. Creativamente hablando, un problema no es un callejón sin salida, sino la puerta a múltiples posibilidades.

Los investigadores de la creatividad descubrieron que el proceso creativo se construye de dos tipos de pensamiento: el divergente que busca nuevas, distintas y muchas ideas; y el convergente, que evalúa, clasifica y elige qué ideas desarrollar. Ambos pensamientos son complementarios pero -y ese fue el gran aporte de los investigadores- deben ir separados. Esto es: cuando damos ideas, no las juzgamos; cuando las evaluamos, no seguimos generando ideas. Solo así se avanza por las distintas fases del proceso creativo de búsqueda de soluciones.
Las fases de la resolución de problemas matemáticos,definidas inicialmente por George Pólya (1) (en el diagrama en color azul), y la resolución creativa de problemas (CPS por sus siglas en inglés) -de Osborn y Parnes en los 50's (2) y distintos modelos posteriores (3) (en el diagrama en color amarillo)-, comparten principios y etapas clave.
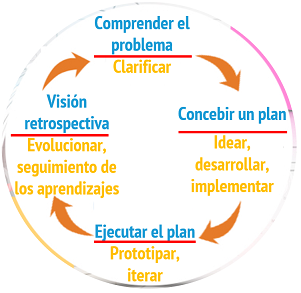
Ambos ciclos requieren:
- Entender el problema (Pólya) / Clarificar (CPS) desafío, usando preguntas que permitan afirmar que comprendieron lo que se está buscado solucionar. En RdP matemáticos, la pregunta que permite definir esta etapa es "¿Entendieron el problema?".
- Diseñar un plan / Idear (investigar, explorar y generar ideas que respondan al desafío); desarrollar (seleccionar las mejores ideas); e implementar (formular un plan). En RdP matemáticos, la pregunta es "¿Tienen una estrategia para resolver el problema?".
- Ejecutar el plan / Experimentar - prototipar (esta etapa está más identificada en el proceso del Pensamiento de diseño o Design thinking; en ella, la estrategia o idea se vuelve tangible a través de un prototipo físico o visible, que sirve para validar si la solución funciona. El proceso que utilizamos para validar es la iteración, repetimos el proceso hasta encontrar una solución que aborde mejor al desafío). En RdP matemáticos, la pregunta es "La estrategia, ¿resuelve el problema?".
- Visión restrospectiva / Evolucionar - hacer seguimiento de los aprendizajes (etapa que también proviene de Design Thinking, refiere a la reflexión y evaluación del proceso, que permite mejorar y avanzar; está asociada normalmente a la comunicación de la solución a otros). La pregunta de la etapa es "¿Qué aprendizajes surgieron durante el proceso?".
El efecto juego
... las fantasías pueden ser malas si hay demasiadas o si están en el lugar equivocado, pero pueden ser buenas por sí mismas y una gran ayuda en la vida y en la solución de problemas. George Pólya
Esta frase nos inspira para plantear el efecto que el juego puede tener sobre el aprendizaje, especialmente de la matemática. El juego permite reducir la ansiedad escolar, al proponer un estado emocional estimulante, donde está permitido probar y equivocarse, sin sanción, sino como parte de la naturaleza del juego, entrenando la tolerancia al fracaso. En este sentido, una forma de comprobar el éxito es que los/as estudiantes tengan una predisposición positiva acerca de la matemática y quieran seguir jugando.
Hay al menos tres características de Creatimat que se nutren del juego
1. El juego y la actitud lúdica están presentes siempre ya que los desafíos matemáticos están insertos en un gran juego y cada desafío se juega.
2. El uso de la fantasía permite acercar mundos lejanos en los diversos escenarios en que los desafíos están contextualizados e involucra a los niños a ser parte de la solución de los problemas que les son significativos, usando la matemática para solucionar problemas.
3. Plantea una metodología gamificada, es decir, que incorpora dinámicas y mecánicas propias del juego, con el objetivo de que niños y niñas tengan una experiencia entretenida e inmersiva de resolución de problemas en contextos reales, experimentando un estado de fluidez. Este concepto introducido por Mihály Csíkszentmihályi, identifica el momento en que las personas están tan inmersas en una actividad que parece que el tiempo "volara", abstrayéndose de todo el contexto.
El ecosistema creativo
Una forma simple de entender la creatividad es definirla como la novedad útil: buscamos nuevas ideas y las que nos ayuden a resolver problemas serán las más bienvenidas. Para lograr esta novedad útil es importante comprender que la creatividad es un fenómeno sistémico y que por lo mismo, se desarrolla mejor en un ecosistema propicio para la creatividad. Creatimat, ayuda a que la sala de clases pueda ser ese ecosistema.
Este ecosistema creativo está compuesto por las personas, procesos, ambiente y productos. En un ecosistema hay relaciones entre las distintas partes y debe también existir un balance.
Las personas
Cuando nos referimos a personas creativas hay ciertas sub habilidades que apoyan el desarrollo personal del potencial creativo, como lo son la originalidad, la flexibilidad, la perseverancia y la curiosidad.
Los procesos
Los procesos tiene relación con los procesos cognitivos en los que nos involucramos para resolver problemas Los procesos pueden combinarse y usarse de distintas formas.. Los dos procesos básicos para el desarrollo de la creatividad son el pensamiento divergente y el pensamiento convergente.
El ambiente
Un ambiente propicio para la creatividad generará el espacio para el desarrollo de personas y procesos quienes así podrán generar productos creativos. Un ambiente creativo es aquel que da espacios para pensar y actuar sin ser juzgados, son espacios seguros, en los cuales se puede compartir y aportar, hay espacio para debate, pero no para conflictos.
Los productos
Para lograr productos creativos es importante valorar la creatividad. Los productos creativos deben ser inusuales e inesperados,
Habilidades creativas
Todas estas herramientas nos permiten diversificarnos como profesores del siglo XXI y preparar a nuestros estudiantes para lo que ellos quieran hacer.
A continuación una descripción de las habilidades que se trabajarán de forma intencionada en cada uno de los desafíos de Creatimat.
Originalidad
Ser original implica ir más allá de los conocido, más allá de las respuestas comunes y atreverse a salir de lo establecido.
Flexibilidad
Desarrollar la flexibilidad tiene todo que ver con adaptarse a los cambios y tomar lo positivo de este cambio. Es saber cuando es necesario cambiar de rumbo y abandonar lo que se estaba haciendo y guardarlo para otra ocasión o abandonarlo para tomar un camino más apropiado para lograr los objetivos.
Perseverancia
La creatividad requiere tiempo, trabajo, sobreponerse a frustraciones y aprender de los errores. La creatividad requiere perseverancia para poder llevar las ideas a término y poder generar valor.
Curiosidad
La curiosidad empieza con buenas preguntas, con datos que no sabías, información inesperada, gatillar la curiosidad es un propulsor de aprendizaje, si logramos encender la chispa de la curiosidad en nuestros estudiantes es más probable que generen aprendizajes significativos.
Referencias
(1) George Pólya: Cómo plantear y resolver problemas
(2) Treffinger, D.; Scott, I.; Stead-Dorval, M.S.: Creative Problem Solving
(3) Ideo: Design thinking para educadores (traducido por educarchile)
(4) Elaborado por Francisca Petrovich, coordinadora equipo Creatimat educarchile
(5) Agencia de Calidad de la Educación: La importancia de las creencias y emociones en el desarrollo personal y académico de los estudiantes

